Miesiąc: czerwiec 2022

Jasne jest, że bezpieczeństwo zapewniane przez schemat klucza publicznego zależy od „odwracalności” procesu od klucza publicznego do klucza prywatnego. Widzieliśmy, że RSA polega na trudności w rozłożeniu dużych liczb na czynniki pierwsze. Inny powszechnie stosowany schemat, opublikowany przez ElGamala, wykorzystuje problem logarytmu dyskretnego, trudności w znalezieniu x, biorąc pod uwagę ostatnią resztę po wielokrotnym dzieleniu ax, gdzie a jest znaną liczbą, przez liczbę pierwszą p. Algorytm ElGamal został wykorzystany do podpisów cyfrowych. Ma niewielką wadę, ponieważ generuje tekst zaszyfrowany, który jest dwa razy dłuższy niż oryginalna wiadomość.

Okazuje się, że choć algorytmy z kluczem publicznym mają tę wielką zaletę znacznie prostszego zarządzania kluczami, w praktyce nie zastąpiły całkowicie algorytmów z kluczami prywatnymi. Systemy klucza prywatnego mają inne zalety, w szczególności szybkość obliczeń. W związku z tym jedną z możliwości jest wykorzystanie systemu klucza publicznego jako bezpiecznego kanału do przekazywania informacji o kluczu prywatnym . Jak pokazano, A może użyć klucza publicznego RSA B do zaszyfrowania klucza prywatnego DES, który będzie używany do bezpiecznej sesji między nimi a B. B może zrobić to samo. Klucze DES są używane do przygotowania kryptowalut DES do użytku przez całą sesję.

Różnice między mnożeniem liczb pierwszych a procesem odwrotnym są podstawą jednego z najbardziej udanych systemów klucza publicznego, RSA, nazwanego na cześć jego wynalazców, Rona Rivesta, Adi Shamira i Leonarda Adlemana. Pełny dowód tej techniki wymaga skomplikowanej matematyki, ale zasada jest prosta. Dwie duże liczby pierwsze o w przybliżeniu równej wielkości są wybierane i mnożone razem, aby otrzymać liczbę o długości kilkuset bitów. Nazywa się to „modułem”. Dwie kolejne liczby są obliczane z dwóch liczb pierwszych. Są to tak zwane klucze publiczne i prywatne. Właściciel musi zachować w tajemnicy wybór dwóch liczb pierwszych i klucza prywatnego, ale może udostępnić moduł i klucz publiczny. Dzięki temu nie ma potrzeby skomplikowanego konfigurowania bezpiecznego kanału do przekazywania tajnych kluczy. Każdy, kto chce wysłać wiadomość, używa algorytmu opisanego poniżej do zaszyfrowania wiadomości, operując na niej za pomocą modułu i klucza publicznego. Gdy wiadomość zostanie zaszyfrowana, zadanie jej odszyfrowania jest równoważne próbie faktoryzacji n, co jest znane jako „trudne”, chyba że ktoś ma dostęp do klucza prywatnego. Znajomość tego klucza prywatnego pozwala uprawnionemu odbiorcy odszyfrować wiadomość przy użyciu podobnego algorytmu do szyfrowania, z wyjątkiem tego, że zamiast klucza publicznego używany jest klucz prywatny.

Algorytm szyfrowania RSA

Algorytm opiera się na wyborze dwóch dużych liczb pierwszych p i q, których tożsamość musi być zachowana w tajemnicy. Niech n = p x q i wybierz liczbę e, która jest mniejsza od n. e nie musi być liczbą pierwszą, ale nie może mieć żadnych wspólnych czynników ani z (p – 1) ani (q – 1) . Musimy teraz znaleźć inną liczbę, d, taką, że (ex d – 1) i podzielna przez (p – 1) (q – 1) bez reszty. Mamy więc trzy liczby: d, e, n. Upubliczniamy e i n. (Są to „klucze publiczne”). D (klucz prywatny) trzymamy w tajemnicy. Załóżmy, że Alicja chce wysłać nam wiadomość, m. Wyszukuje naszą wartość e na liście publicznej. Następnie podnosi m do potęgi e. (Oznacza to, że mnoży m przez siebie, e razy. Gdyby m było „345”, a e było „7”, obliczyłaby 345 x 345 x 345 x 345 x 345 x 345 x 345). Następnie znajduje n z listy publicznej i wielokrotnie dzieli je na poprzednie obliczenia, aż pozostanie tylko reszta R. (np. załóżmy, że m do potęgi e = 10n + R. W notacji matematycznej jest to znane jako znalezienie R = m^e mod n). R to zaszyfrowany tekst, który Alicja wysyła do nas przez otwarty kanał. Można wykazać, że każda technika, która pozwala znaleźć m na podstawie R i znajomości n i e, jest trudna obliczeniowo, równoważna próbie rozłożenia na czynniki iloczynu dwóch liczb pierwszych. Bierzemy zaszyfrowany tekst R i podnosimy go do potęgi d (klucz tajny). Następnie znajdujemy resztę po wielokrotnym dzieleniu przez n (tj. obliczyliśmy Rd mod n). Co zaskakujące, okazuje się, że jest to m, wiadomość tekstowa. Typowa wartość klucza publicznego, zakodowana jako ciąg alfanumeryczny, wyglądałaby mniej więcej tak

Wszystkie systemy, które omówiliśmy powyżej, miały na celu osiągnięcie wysokiego stopnia bezpieczeństwa z łatwym do zarządzania układem obsługi kluczy. Ale wszyscy mają wspólny problem, że nadal musi istnieć bezpieczny kanał dostarczania tajnych kluczy. Jest to przykład stosunkowo bezpiecznego, algorytmicznie bezpiecznego systemu, który może zostać naruszony przez uciążliwy proces bezpieczeństwa. Na pierwszy rzut oka wydaje się to nieuniknionym wymogiem; jeśli odkryjesz klucz, którego używam do zaszyfrowania wiadomości, to na pewno łatwo ci go odszyfrować? To prawda, jeśli klucz do odszyfrowania wiadomości jest albo identyczny z kluczem szyfrowania, albo łatwo go z niego wyprowadzić, a metoda odszyfrowania polega na prostym odwróceniu szyfrowania. Ale załóżmy, że tak nie jest? W tym przypadku okazuje się, że istnieje szereg technik, które otwierają zaskakującą możliwość. Możliwość otwartego publikowania klucza szyfrowania dla każdego, co nie ułatwia nikomu poza wystawcą klucza odszyfrowania wiadomości zaszyfrowanych tym kluczem. Aby zrozumieć, co to oznacza, rozważ przykład pokazany na rysunku

Bob chce wysłać tajną wiadomość do Alice. Zauważa, że ​​Alicja powiedziała światu swój klucz publiczny. Używa tego do zaszyfrowania swojej wiadomości, zgodnie z jednym z algorytmów, które omówimy później. Następnie wysyła do niej swoją wiadomość przez otwarty kanał, wiedząc, że nawet jeśli Charlie zdoła ją przechwycić, nie będzie w stanie jej zrozumieć. Jednak Alicja i tylko Alicja, która posiada klucz prywatny, który działa jako odwrotność klucza publicznego i którego pilnie strzeże dla siebie, może zostać wykorzystana do odszyfrowania wiadomości. Ze względu na specjalną relację między kluczami prywatnymi i publicznymi Charlie jest niezwykle trudny do odszyfrowania wiadomości i opracowania klucza prywatnego. Być może bardziej zaskakujące jest to, że nikt, nawet Bob, nie może wrócić od znajomości wiadomości i klucza publicznego do prywatnego. Systemy szyfrowania klucza publicznego opierają się na fakcie, że niektóre operacje matematyczne są łatwe do wykonania w jednym kierunku, ale trudne w innym. Jednym z przykładów jest formowanie kwadratu liczby – prosta operacja mnożenia samej liczby – w porównaniu z otrzymaniem wyniku i poproszeniem o znalezienie pierwiastka kwadratowego. Liczba wymaganych do tego kroków jest znacznie większa niż w przypadku operacji kwadratu. Inną, bardziej odpowiednią operacją jest „faktoryzacja iloczynów liczb pierwszych”. Przypominamy sobie, że liczby pierwsze to liczby całkowite, których nie można „rozłożyć na czynniki” na iloczyn liczby mniejszych liczb całkowitych. 1, 2, 3, 5, 7 to liczby pierwsze, ale nie 4 (= 2 x 2), 6 (= 2 x 3) lub 9 (= 3 x 3). Wiadomo, że istnieje nieskończona liczba liczb pierwszych, z których około 10¹⁵⁰ ma 512 bitów lub mniej, ale nie ma znanego wzoru na udowodnienie, ogólnie, że liczba jest lub nie jest liczbą pierwszą, co jest znacznie szybsze niż próba lub błąd. Czas potrzebny na wykonanie tego rośnie bardzo szybko wraz z wielkością liczby. Podobny problem dotyczy „rozkładania na czynniki iloczynu dwóch liczb pierwszych”. (tj. znalezienie p i q, mając tylko p czas q). Łatwo jest pomnożyć dwie liczby pierwsze, ale trudno odwrócić ten proces.

Niezależnie od tego, czy DES ma słabości, czy nie, nadal lepiej polegać na nim niż na wielu innych systemach, które nie były intensywnie atakowane. W każdym razie równowaga między atakującym a obrońcą nie stoi w miejscu. Jednym z problemów radzenia sobie z postępami w technologii ataku jest zachowanie wstecznej kompatybilności ze starszymi systemami. Zamiast wyrzucać DES, wprowadzać nowy system i ponownie wpisywać wszystkie dane, istnieje tendencja do wydłużania czasu pracy DES poprzez wprowadzenie dłuższego klucza. W rzeczywistości zaproponowano trzy klucze 56-bitowe zamiast jednego, pod nazwą potrójnego DES. Szczególnie preferowaną opcją jest użycie tylko dwóch różnych kluczy, przy czym jeden z nich zostanie zastosowany dwukrotnie. Zdarza się, że dzięki temu odszyfrowanie może być zasadniczo odwróceniem szyfrowania. Niezależnie od rzeczywistych lub wyobrażonych słabości DES, w świecie, w którym nic nie jest pewne, prawdopodobnie prawdą jest, że potrójny DES jest bezpieczniejszy niż praktyczne zarządzanie jego kluczami. Przyjrzyjmy się teraz, jak można złagodzić niektóre problemy z zarządzaniem kluczami .

Jednym z opublikowanych i szeroko stosowanym przykładem systemu szyfrowania Feistal jest Data Encryption Standard (DES). Używa to zwykle klucza o długości co najmniej 56 bitów. Daje to prawie 1017 możliwości, które atakujący musiałby spróbować w ataku brute force. Dobrze zaprogramowany komputer ogólnego przeznaczenia w dzisiejszej technologii zajęłoby około stu lat, aby przetestować każdą możliwość. Podwojenie długości klucza do 128 bitów wydłuża czas szyfrowania o tę samą kolejność, ale sprawia, że ​​atak brute force jest 1020 razy dłuższy. Wymagałoby to imponująco dużej mocy obliczeniowej, gdyby został zaatakowany przy użyciu jednego konwencjonalnego komputera, ale uważaj, istnieją inne sposoby na zrobienie tego. Jedna z propozycji przewiduje bardzo dużą populację patriotycznych chałupników i poziom niezbyt drogiej, ale szeroko rozpowszechnionej technologii. Pojawienie się nadawania satelitarnego w Chinach zasugerowało szczególną technikę i nazwę chińska loteria. Atakujący przechwycił łącze i przesłał sygnał na satelitarnym kanale nadawczym do wielu milionów domów, z których każdy wyposażony jest w telewizor i dekoder satelitarny w postaci dekodera. Ten ostatni jest zasadniczo zmodyfikowanym komputerem i można go po prostu dalej zmodyfikować, aby umożliwić włączenie algorytmu kryptograficznego. Klucze wybrane losowo przez każde gospodarstwo domowe są testowane, aby sprawdzić, czy na ekranie telewizora pojawia się znaczący komunikat. Jedna z wielu milionów prób wkrótce zakończy się sukcesem. Okazało się, że jeden z najwcześniejszych udanych ataków na zaszyfrowaną wiadomość przy użyciu tej techniki został dokonany nie dzięki wielkiemu aktowi patriotycznej solidarności, ale dzięki ochotniczej sile 14 000 internautów, z których jednemu udało się znaleźć 56-bitowy klucz. Poprzedni sukces z użyciem 3500 komputerów osobistych złamał 48-bitowy klucz w 13 dni. Poważne implikacje są takie, że ataki oparte na przetwarzaniu równoległym zawsze będą stanowić zagrożenie dla wszelkich technik szyfrowania. Oszacowano, że kosztujące mniej niż milion dolarów maszyny specjalnego przeznaczenia, które przeprowadzają dużą liczbę równoległych ataków na 56-bitowy DES, mogą osiągnąć sukces w ciągu kilku godzin. To mieści się w granicach bezpieczeństwa rządu wielu narodów (i prawdopodobnie kilku globalnych syndykatów przestępczych). Istnieje również ciągła teoria spiskowa, według której DES zawiera słabość, która została celowo wprowadzona przez Agencję Bezpieczeństwa Narodowego, ale pomimo wielu prób czołowych ekspertów sprzeciwiających się „ingerencji” rządu, nie opublikowano żadnych sukcesów, a historia musi być traktowana z pewnym sceptycyzmem. Zaproponowano inne ataki, które wykorzystują ataki z tekstem jawnym, w których atakującemu udaje się albo skłonić nadawcę do zakodowania wybranych przez niego wiadomości, albo po prostu użyć wiadomości, których tekst jawny jest znany. Jeden z przykładów tego ostatniego z powodzeniem odzyskał klucz w ciągu 50 dni przy użyciu 12 stacji roboczych, ale wymagało to 2⁴3 znanych tekstów jawnych, a zatem prawdopodobnie nie jest praktyczne.

Podany powyżej opis szyfru Feistela sugeruje, że dane muszą istnieć w blokach o określonej wielkości, współmiernej do wielkości klucza. W rzeczywistości nie jest to wymóg; możliwe jest wykorzystanie zasady Feistela do generowania szyfrowania na każdym pojedynczym bicie danych wejściowych. W przykładzie omówionego wcześniej liniowego schematu szyfrowania rejestru przesuwnego, Rysunek pokazuje rejestr przesuwny działający w trybie sprzężenia zwrotnego, w którym rejestr generuje strumień danych pseudolosowych, który jest OR’d z danymi jawnego tekstu.

Możemy zrobić dokładnie to samo z szyframi Feistela, torując pole zmiany kolejności sekwencją początkową, pozwalając mu zaszyfrować to za pomocą klucza i w ten sposób wytwarzając zestaw bitów wyjściowych, z których niektóre można ORAZ z danymi do być zaszyfrowane. Bity wyjściowe z pola zmiany kolejności można następnie przesłać z powrotem do skrzynki, aby wygenerować nową sekwencję. Istnieje również kilka sposobów na zaimplementowanie podstawowego szyfrowania blokowego szyfru Feistela. Na przykład możliwe jest LUB poprzednie wyjście zaszyfrowanego tekstu z bieżącym blokiem. Ma to tę zaletę, że atakującemu trudniej jest wykorzystać powtarzające się bloki identycznych danych. Jednak, jak wszystkie odmiany, ma również wady. Musimy pamiętać, że atakujący mogą teoretycznie wstrzykiwać własne wiadomości w celu zainicjowania znanego ataku tekstowego lub mogą wprowadzić błędy, które mogą rozprzestrzeniać się na kilka bloków danych, czyniąc system bezużytecznym, a uprawnione strony mogą chcieć cofnąć do niepewnej alternatywy.

Alternatywą dla szyfrów strumieniowych są szyfry blokowe, które operują na bloku danych o ustalonej liczbie bitów w celu uzyskania równoważnego, zaszyfrowanego wyjścia. Zamiast generować oddzielny strumień bitów pseudolosowych i łączyć je z tekstem jawnym, szyfry blokowe często wykonują operacje „szyfrowania” na samych danych w postaci zwykłego tekstu, zmieniając kolejność bitów w bloku i łącząc je z innymi bitami, na przykład za pomocą funkcji OR . Alternatywnie, możemy po prostu wziąć duży blok danych i zaszyfrować kolejność bitów, zgodnie z pewnym wzorem permutacji, znanym nadawcy i odbiorcy, ale ponownie utrzymywanym w tajemnicy przed innymi. Kilka przykładów opiera się na szyfrach Feistela, które wielokrotnie przekazują tekst przez tę samą funkcję szyfrującą. Blok danych w postaci zwykłego tekstu jest podzielony na pół. Połowa danych jest obsługiwana przez funkcję F, która dokonuje zmiany kolejności (tasowania) bitów w bloku, zgodnie z „podkluczem” (SK1). Wynik ponownego uporządkowania jest następnie „LUB” z niepoddaną obróbce połową. Połówki są następnie zamieniane i ta sama funkcja zmiany kolejności została zastosowana do drugiej połowy. Należy zauważyć, że funkcja zmiany kolejności jest nadal taka sama, ale jej wpływ na dane może być inny, ponieważ jest kontrolowany przez nowy podklucz (SK2). Proces można powtarzać w kółko. Szyfry Feistela są wygodne do odszyfrowania, ponieważ proces szyfrowania jest po prostu odwrócony, stosując podklucze w odwrotnej kolejności. Funkcje zmiany kolejności są tak dobrane, że ich szczegółowe działanie na danych jest trudne do odszyfrowania bez znajomości podkluczy. W ten sposób funkcje ponownego porządkowania mogą być upublicznione.

Oczywiście potrzebujemy bardziej praktycznego rozwiązania. Osiąga się to poprzez poświęcenie doskonałego bezpieczeństwa na rzecz znacznie krótszego klucza i bardziej złożonego krypto. Istnieje wiele sposobów na osiągnięcie tego. Niektóre opierają się na zasadzie generowania liczb, które wydają się losowe, które są następnie używane zasadniczo w taki sam sposób, jak klawisze jednorazowego bloku. Inne tasują (permutują) dane w wiadomości w kolejności opartej na pozornie losowym kluczu. Bardzo prostym przykładem tego pierwszego (który jest bardzo ubogi pod względem kryptograficznym) jest rejestr przesuwny z liniowym sprzężeniem zwrotnym. Rejestr przesuwny umożliwia sekwencyjne przesuwanie wzorców bitowych od lewej do prawej. W pokazanym urządzeniu niektóre z tych bitów są również odczepiane i przekazywane przez zamknięte przełączniki (2, 5 i n) do urządzenia funkcyjnego „LUB”. Funkcja LUB wykonuje serię operacji dodawania połowy (0 + 0 = 1 , 0 + 1 = 1 , 1 + 1 = 0) na danych, tak że parzysta liczba jedynek da odpowiedź 0, a nieparzysta number da 1. Odpowiedź brzmi ‘OR’d’ z pierwszym bitem tekstu jawnego, tym samym szyfrując go. Odpowiedź jest również „sprzężenie zwrotne” do lewej komórki rejestru przesuwnego po tym, jak wszystkie inne bity w niej przesunęły się o jedno miejsce w prawo. To jest przykład szyfru strumieniowego: strumień pseudolosowych bitów jest generowany przez krypto i dodawany bit po bicie do kolejnych bitów zwykłego tekstu. Możliwe jest wykazanie, że prawowici odbiorcy danych mogą je odszyfrować za pomocą podobnego urządzenia, pod warunkiem, że wiedzą, które przełączniki są zamknięte i sekwencję startową (w tym przypadku 110100). „Krypto” składa się z przesunięcia rejestru i generatora funkcji (w tym przypadku funkcja OR). Należy założyć, że atakujący może mieć przynajmniej pewną wiedzę na temat liczby stopni w rejestrze przesuwnym i natury generatora funkcji. Jedynym zabezpieczeniem, jakie można założyć, jest zabezpieczenie zawarte w kluczu. W tym urządzeniu klucz składa się z dwóch elementów: sekwencji startowej i ustawień przełącznika. Muszą one być wymieniane między nadawcą a odbiorcą za pomocą bezpiecznego kanału (na przykład zaufanego posłańca) i utrzymywane w tajemnicy, dopóki nie będzie można użyć nowego zestawu. Praktyczne systemy wykorzystują funkcje inne niż pojedynczy rejestr przesuwny ze sprzężeniem zwrotnym i prostą funkcją OR. Podczas gdy pojedynczy rejestr przesuwny zapewnia pewne bezpieczeństwo, gdy atakujący nie ma wiedzy o treści wiadomości, jest bardzo słaby, gdy część tekstu jest znana lub można ją odgadnąć. (Na przykład wiele liter zaczyna się „Szanowny Panie”, zawiera datę lub kończy się równie konwencjonalnie.) W tym przypadku można wykazać, że system zawsze może zostać uszkodzony, mając mniej niż 10N kolejnych bitów tekstu jawnego, gdzie N to liczba etapów w  rejestrze przesuwnym. Należy z tego wyciągnąć dwa ważne punkty: po pierwsze, systemy kryptograficzne muszą brać pod uwagę zarówno praktyczność, jak i teorię, a w szczególności możliwość, że atakujący zaczyna mieć więcej niż zerową wiedzę. Po drugie, krytycznym czynnikiem projektowym jest stosunek wysiłku atakującego do wymaganego przez uprawnionych użytkowników. To, co musimy osiągnąć, to przedstawienie atakującemu stopnia trudności, który rośnie szybciej niż jakikolwiek wzrost złożoności krypto. Nie jest to prawdą w przypadku rejestru przesuwnego, gdzie złożoność systemu i jego podatność na ataki rosną „liniowo”, to znaczy z N. Chcielibyśmy, aby system, którego złożoność można było zwiększyć o N, z wynikający z tego wzrost trudności ataku o (przynajmniej) N^M, gdzie M jest pewną dużą liczbą. Niektóre praktyczne alternatywy oferujące lepsze zabezpieczenia obejmują kaskady rejestrów przesuwnych, których tryby działania oddziałują na siebie. Na przykład możemy wykorzystać wyjście jednego rejestru do sterowania zegarem sterującym następnym; to znaczy sprawić, by poruszał się na więcej niż jednej zmianie na raz.

pierwszy rygorystycznie przeanalizowany podczas ostatniej wojny, w szczególności przez Claude’a Shannona z Bell Laboratories. Kiedy spotykamy się z tymi badaniami po raz pierwszy, może nas zaskoczyć, że nie były one skoncentrowane na tworzeniu coraz silniejszych szyfrów. W rzeczywistości głównym postępem, jaki dokonał Shannon, było udowodnienie, że chociaż istniał „doskonały” szyfr (w tym sensie, że nie można go złamać, pod warunkiem, że był wspierany przez silną implementację), w większości przypadków to wdrożenie byłoby niewykonalne. Ten doskonały szyfr znany jest pod różnymi nazwami, ale najczęściej jako jednorazowy pad. Według okazjonalnych doniesień publicznych, znajduje co najmniej jedno praktyczne zastosowanie – jako środek komunikacji między szpiegami a ich kontrolerami. Oto, koncepcyjnie, jak to jest używane:

Litery wiadomości (tekst jawny) są najpierw zamieniane na liczby: A = 1, B = 2 i tak dalej.

Więc; Sekretariat

staje się 19 5 3 18 5 20

Agent szyfrujący posiada zestaw stron zawierających listy liczb z zakresu od 1 do 26, które zostały wygenerowane losowo: 21, 3, 13, 19, 5, 7 itd. Te z kolei są dodawane do liczb odpowiadających do tekstu jawnego. Jeśli suma przekracza 26, odejmuje się 26. Daje to zaszyfrowany tekst:

19 5 3 18 5 20

plus 21 3 13 19 5 7 daje

szyfrogram =14 8 16 11 10 27

Jeśli liczby zostały naprawdę wygenerowane losowo, nie ma możliwości, aby urządzenie przechwytujące mogło wrócić do tekstu jawnego. Jeśli jednak prawowity odbiorca ma kopię liczb losowych i wie, gdzie się zaczynają, łatwo jest je odjąć od zaszyfrowanego tekstu (a następnie dodać 26, jeśli wynik jest ujemny), aby wrócić do tekstu jawnego:

szyfrogram 14 8 16 11 10 27

minus 21 3 13 19 5 7 daje

tekst jawny 19 5 3 18 5 20

czyli SE C R E T

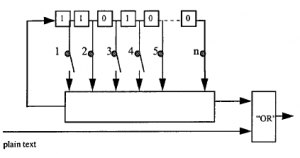
„Klucz” metody składa się z określonych liczb na podkładce; „krypto” to po prostu operacja dodania klucza do wiadomości. Chociaż jest to najbezpieczniejszy z możliwych system, jednorazowy pad ma poważny problem: rozmiar pada musi być taki sam, jak całkowita liczba znaków we wszystkich wiadomościach, które chcesz wysłać. Nie jest dobrym pomysłem ponowne użycie zestawu liczb: atakujący może połączyć inteligentne zgadywanie z dość prostymi statystykami, aby skutecznie złamać szyfr. To może nie być problem, gdy wiadomości, które chcemy wysłać, są krótkie i rzadkie. Kontroler i szpieg mogą prawdopodobnie umawiać się na wystarczająco częste spotkania, aby przekazać nowe jednorazowe podkładki. Jeśli jednak chcemy zapewnić wygodny mechanizm płatności międzybankowych, obejmujący miliony transakcji tygodniowo, trudno wyobrazić sobie wysyłanie kurierów po całym świecie z ryzami jednorazowych bloczków. Albo rozważmy przypadek próby zaszyfrowania programu telewizyjnego, aby mogli go oglądać tylko opłaceni widzowie: potrzebowalibyśmy jednorazowych padów zapewniających każdemu abonentowi telewizyjnemu kilka megabitów na sekundę.