Matematyczne metody dopasowywania wzorców mogą być bardzo złożone i trudne do zrozumienia. Być może najbardziej dostępną metodą jest „klasyfikacja liniowa”. Ponieważ większość jego zasad można zastosować do innych, bardziej złożonych technik, przyjrzymy się jej nieco szczegółowo. Załóżmy, że decydujemy się na prosty schemat rozpoznawania pisma ręcznego. Rozważ problem rozpoznania autorstwa odręcznej litery „W” na rysunku
Dla przykładu rozważmy, że zdecydowaliśmy się zmierzyć dwie cechy listu:
† Średnie nachylenie suwu w dół AB.
Szybkość płyty CD w górę.
Załóżmy, że mamy kilka przykładów W napisanych przez każdą z N osób. Nie wszystkie będą miały taką samą wartość, ani dla wszystkich pisarzy, ani nawet dla każdej osoby. Załóżmy, że wykreślamy wartości na wykresie, jak pokazano na rysunku.
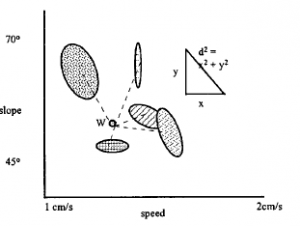
Każda z pięciu elips reprezentuje pierścień wokół większości wartości dla każdego pisarza. Widzimy, że dla wszystkich pisarzy wartość nachylenia waha się od około 45-708, a prędkość od około 1 do 1,5 cm/s. Widzimy również, że istnieje pisarz tajemnicy „W”. Aby uczynić rysunek 2.32 bardziej czytelnym, celowo wybraliśmy pozycję dla W, która jest daleko od centrum wartości dla dowolnego autora, ale będziemy nalegać, aby W musi być jednym z nich. Ale który? Naszą pierwszą myślą jest po prostu zmierzenie długości linii między różdżką i środkami rozrzutu wartości każdego pisarza i wybranie znanego pisarza, który jest najbliżej. Na wykresie dwuwymiarowym
Odległość = pierwiastek kwadratowy z (x odległość do kwadratu + y odległość do kwadratu)
zgodnie z twierdzeniem Pitagorasa. Zauważ, że gdybyśmy mieli trzy różne zmierzone parametry, a nie dwa, wzór można łatwo rozszerzyć, dodając wyraz w z-kwadrat. W rzeczywistości można go rozszerzyć, aby obejmował tyle „wymiarów”, ile chcemy, dodając termin dla każdego. Ale to nie jest takie proste. Wracając do naszego dwuwymiarowego przykładu, załóżmy, że po prostu zmieniliśmy skalę poziomą z cm/s na m/s lub pionową ze stopni na radiany? Względne odległości ulegną zmianie i może się okazać, że teraz utożsamiamy W z kimś innym. Zamiast używać arbitralnych skal, musimy wybrać skalę, która uwzględnia zależność między rozrzutem wartości dla każdej cechy u wszystkich autorów, w porównaniu ze średnim rozrzutem dla każdej cechy u jednego autora. Definiujemy stosunek, umownie nazywany stosunkiem F:
F = zakres wartości mierzonej cechy; przez wszystkich pisarzy / średnie wariacje poszczególnych pisarzy
Krótka myśl wyjaśni, że to obliczenie, zastosowane do każdego wymiaru („cecha”), da oszacowanie dyskryminującego moc wymiaru, duży współczynnik F, co oznacza, że dana funkcja jest wysoce skuteczna w rozróżnianiu pisarzy. W praktyce współczynnik F jest używany jako czynnik ważenia przy obliczaniu odległości między nieznanym przykładem a różnymi możliwymi pisarzami. Można wykazać, że usuwa to wszelki wpływ określonych jednostek (takie jak centymetry kontra metry). Jest jeszcze inny, bardzo ważny aspekt współczynnika F: zwykle łatwiej jest ustalić zaufanie do elementu systemu, jeśli jego współczynnik F jest wysoki, jak zobaczymy w poniższych przykładach.